Circle Of Fifths Diagram
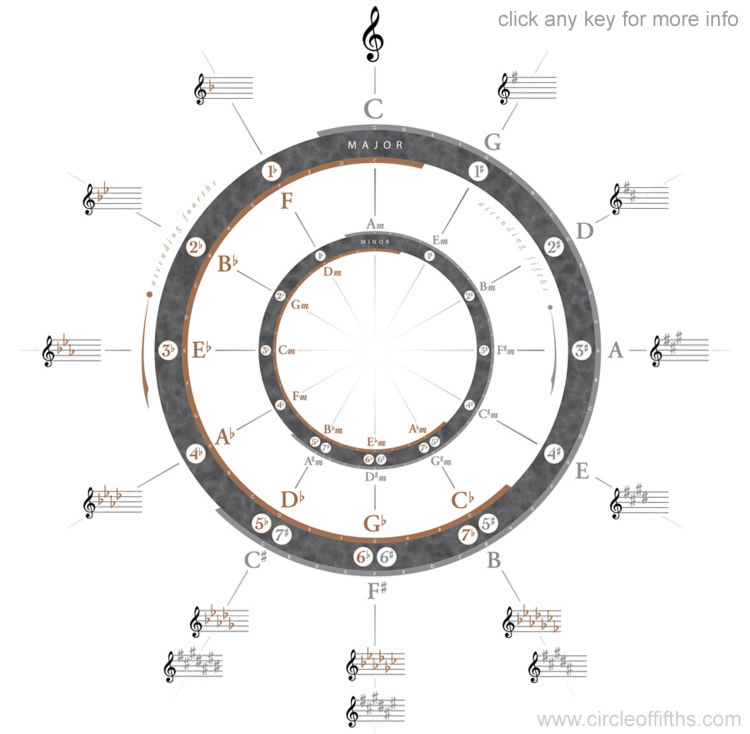
The circle of fifths diagram reveals several important musical relationships and is one of the most important tools available to a musician. The circle of fifths diagram shows the relationship between major and natural minor keys as well as the most frequently used intervals for chordal harmonic movement. The circle (or cycle) of fifths, also called the cycle of fourths is a diagram that gives all kind of handy information on key signatures, chords and scales in a quick and clear manner. Besides that, it’s an awesome practice tool to improve your guitar playing. The circle displays all 12 notes of the chromatic. The circle of fifths Infographic The circle of fifths is a visual representation of the keys you hear in music. Starting at the top with the key of C major. The circle is split between the sharps (right side) and flats (left side) we encounter as we travel around it. Diagram 1 - Quick Progression Circle of Fifths Generator: (above example is in the key of A Major) At the reference area you’ll find a link that will allow you to instantly create chord progressions based on the Circle of Fifths in every single key, but the generator focuses more on the actual. The Circle Of Fifths. The circle of fifths is a tool used by musicians and songwriters to find the number of sharps or flats are in a key. This is vital to know and should be memorised for fast key recognition. As you’re moving clockwise around the circle, keys jump up by a fifth (hence the name). As you can see in the diagram, each time you.
1. Circle of fifths - why is it useful ?
The Circle of fifths diagram shows the most commonly used major and (natural) minor scales used in music theory. It is useful for the following reasons, so far as scales are concerned:
a) It is easy to build and construct scale note names
Using the system described in the remainder of these lessons (lessons 2, 3, 4 and 5), when drawing the diagram from a blank sheet of paper, it is easy to work out which notes are in every scale shown in the diagram. ie. which scales have sharps or flats, their note names, and how many sharps and flats there are in each scale.
By following the system below, you will not need to know in advance which notes are in which scales before you draw the diagram - all note names will naturally fall out as part of the process of drawing the diagram.
It is arguably much easier to learn to draw this single diagram than calculating and memorizing the notes in all 30 scales individually (and manually).
For an example on how to construct a scale manually, have a look at any major scale eg. Gb major scale, which shows the process of arriving at the note names by using tone-semitone intervals, then deciding the note names. It is not always straightforward, especially when certain white notes need to be sharpened or flattened and renamed completely.
b) It shows scales that are similar to each other in name, and sound
Not only does the Circle of 5ths show all the most useful scales, but it shows which scales sound similar to each other.
It groups together different scales which differ only by one note name (a sharp or a flat), and it also groups together those scales where a major and minor scale actually contain the same note names.
It also groups together scales which have different names eg. F-sharp major and G-flat major, which contain different note names, but the note pitches ie. note sounds are identical.
This is useful when composing music and being able to quickly identify which chords and scales sound good together.
c) It makes basic music theory concepts hang together in a logical way
This system for drawing the Circle of fifths uses easy-to-remember phrases / facts to show the placement of the scale names, so the diagram can be drawn without knowing anything about musical theory (scales etc.) beforehand.
This is useful to get the diagram completed, but it is not a very musical way of understanding the relationships between scales grouped together on the diagram.
So as part of the process of drawing the diagram, this system will describe the musical intervals that underpin all the circle of fifths relationships - specifically the importance of the 3rd, 4th, 5th and 6th scale notes as entrypoints into related and similar scales.
The Circle of fifths diagram below shows the major and minor scale names, including a table at the bottom showing the sharp and flat notes in each scale (highlighted with yellow bullets).
It might be useful to save it and print it off the diagram for reference.
The rest of the Introduction below explains the diagram structure in detail.
2. Circle of fifths diagram structure
a) Common Vs Theoretical scales
The Circle of fifths shows the most common and popular major and minor scales to use for composing music.
Every scale on this diagram contains notes having only single sharps and flats.. never double-sharps or flats, which are messier to work with.
In contrast, other scales do exist in theory (called theoretical scales), but these are just identical scales to those already on the Circle of fifths diagram, but with different scale names, and with double-sharps or flats - much more complex to work with.
As a specific example, have a look at the key signature of the A# major scale, which has 3 double-sharps plus 4 Single sharps(!), and then have a look at the construction of the Bb major scale, which has just 2 flats.
Then have a look at Step 3 of both these pages - showing the tone / semitone intervals and starting note, and it is clear that although both of these scales contain different note names, they use exactly the same note pitches. ie. the same physical piano keys are pressed in both scales.
This means that given a choice, the B-flat major scale would be used in preference to A-sharp to describe a set of note pitches on a musical staff. From a music theory perspective, Scales A-sharp and B-flat are said to be enharmonic to each other, as they contain the same note pitches.
The harmonic minor and melodic minor scales, both derived from the natural minor scales are not shown on the diagram.
b) The Spiral of fifths Vs The Circle of fifths
The Circle of 5ths diagram above is based on the Wikipedia version by Just plain Bill, except that it is shown as a spiral, with the sharps and flats clearly separated out at the 5, 6 and 7 o'clock positions, where the spiral arms overlap.
Even though the circle is shown as a spiral, the idea of it being a clock with 12 hour positions still holds.
The letter names in red refer to major scales, so at 12 o'clock, the C note means the C major scale.
The letter names in green refer to minor scales, so at 12 o'clock, the A note means the A natural minor scale.
The minor scales are shown in lower case just to clearly separate them out from the major scales - normally the A minor scale would be abbreviated to Am, but the m is left off to keep it uncluttered.
So for example, at 9 o'clock two scales are shown - Eb major scale (red), and the C natural minor scale (green).
An example where the spiral arms overlap is at 5 o'clock, which has 4 scales at this hour position: Cb major scaleand the B major scale (both red), and the Ab natural minor scaleandG# natural minor scale (in green).
c) Black spiral dots - number of sharps or flats, the related minor
Every spiral position (black dot) contains black text saying how many sharps or flats the red major and green minor scales have around it.
For example, at 4 o'clock, it says that the E major scale and the C# natural minor scale both contain 4 sharps.
Importantly, from a music theory perspective, both of these scales contain the same note names, and so the only difference between them is that they start on a different note, the (tonic, or starting note).
For example, E major starts on note E, and C-sharp minor starts on note C#, but both scales contain the notes E, F-sharp, G-sharp, A, B, C-sharp, and D-sharp, but in a different order.
This relationship is called the related minor (or relative minor). As an example, have a look at the E relative minor page.
d) The spiral structure - from 7 sharps to 7 flats
The C# major scale and A# natural minor scale both have all notes sharpened (7 in total), and they begin on the inner arm of the spiral, at 7 o'clock, and then moving counter-clockwise (7, 6, 5 etc.), the number of sharps decreases by one each time until C major scale and A natural minor scale at 12 o'clock, which both have no sharps or flats.
At 12 o'clock, C major and A minor are unique cases in being the only scales on the Circle of 5ths diagram that have no sharps or flats.. only white keys are used to play them. They are shown with a natural symbol next to the zero to indicate no sharps or flats.
Then continuing counter-clockwise from C major, the number of flats starts increasing from 1 to the end of the outer arm of the spiral at 5 o'clock, whose scales Cb major scale and Ab natural minor scale have all 7 notes in the scale flattened.
Circle Of Fifths Diagram Pdf
e) Each hour is one note away from its neighbors
Circle Of Fifths Diagram With Double Sharps
Every hour position contains scales which are 1 sharp or 1 flat , ie. one note different from the previous and next hours.
Circle Of Fifths Diagram Pdf
This arrangement is useful, because scales that are similar to each other, and chords based on those scales also sound good together.
For example the C, F and G major chords (hour positions 12,11,1) sound great together, and this progression is used a lot in pop music.
The scales at the same hour position (the relative minor) are also important in identifying similar scales.
For example, looking at 12 o'clock, the relative minor of C major scale is A natural minor scale
So extending the chords sequence given just slightly, it is no coincidence that the C, Am, F and G is another very popular pop chord progression.
The further around the circle relative to a given hour, the fewer notes there will be in common, and so the more awkward or dissonant the chords will sound together.
For example, scale D and A-flat (8 o'clock) would struggle to sound good when played next to each other.
The example above uses major scales, but obviously the same principle applies to the minor scales, who are separated by one note for each hour position.
f) Spiral arm overlap at 5,6,7 o'clock, enharmonic scales
For any given point on the spiral, the major/related minor scales contain the same note names, but arranged in a different order.
So on the outer arm, we can say that at 6 o'clock, Gb major scale has the same note names as Eb natural minor scale, and on the inner arm, F# major scale has the same note names as D# natural minor scale.
So what is the significance of the spiral arms overlapping in this way, so far as the scales notes are concerned?
Looking at the two major scales at 6 o'clock, we see the note names F# and Gb.
These are really different note names for the same physical black key on the piano, and so a major scale built starting from that physical piano key will have the same note pitches/sounds, regardless of whether that tonic/starting note is called F-sharp or G-flat.
So it turns out that these scales have identical note pitches/sounds, and only differ by the note names used by each.
F# major scale uses 6 sharp names, and Gb major scale uses 6 flat names, but they sound identical, as the Tone-Tone-Semitone-Tone-Tone-Tone-Semitone intervals used to construct this scale remain the same whether we choose to call the first note in the scale F-sharp or G-flat.
To see this in action, compare how F-sharp and G-flat are constructed, and you can see that steps 1 to 3 on these pages are identical in terms of which white and black piano keys are used to decide the 7 notes in the scale. Steps 4 onwards are different, where the note names are decided as being sharp or flat.
This property of having two note names for the same note pitch is called enharmonic, and in music theory terms, we would say that the F-sharp scale is enharmonic to the G-flat scale. Either scale could be used to represent the note pitches you can play and hear.
The same applies to the two minor scales at 6 o'clock - D# natural minor scale and Eb natural minor scale are enharmonic to each other, with the same note pitches/sounds, but different note names.
g) Drawing the Circle of fifths diagram
That concludes the music theory needed for the remaining 4 lessons.
These lessons will each take a portion of the Circle of fifths diagram, draw in the scale names, and then work out the notes in each scale.
To continue, click on the 2. Major sharps link below.
| Lesson | 1. Introduction | 2. Major sharps | 3. Minor sharps | 4. Major flats | 5. Minor flats |
|---|
This tutorial is a companion resource of the Interactive Circle Of Fifths Tool , a music learning software available on this site. The Circle Of Fifths , also called Cof , was invented in the 1670s by Nikolai Diletskii in his 'Grammatika'; this incredible device embeds all the music theory you need to know for doing a lot of funny things.
Indeed, at the end of this tutorial, you'll be able to use the Circle of Fifths to:
- Identify sharps and flats for each music key
- Know the chords that belong to a key
- Create chord progressions
- Modulate to other keys
- Construct chords of different types
Don't feel overwhelmed by such amount of information, the Circle of Fifths makes it easy to understand and master the tasks listed above.
You may want to open the Interactive Circle Of Fifths on a separate page so that you can follow this tutorial and experiment the concepts with the tool.
Are you ready?
Let's unveil the hidden mysteries of the Circle Of Fifths!
Did you already download your free pdfs?
Download Your Free Learning Resources
Table Of Contents
These maps show you the tones in a chord all along the fretboard. They are incredibly helpful because allow you to:

- Create new voicings on the fly, across all the neck
- Improvise targeting the right notes
- Unlock the fretboard and expand the CAGED system.
In the new ebook, Chords Domination, you'll find the fretboard tones maps for 44 different qualities of chords. Check it out:
Introduction
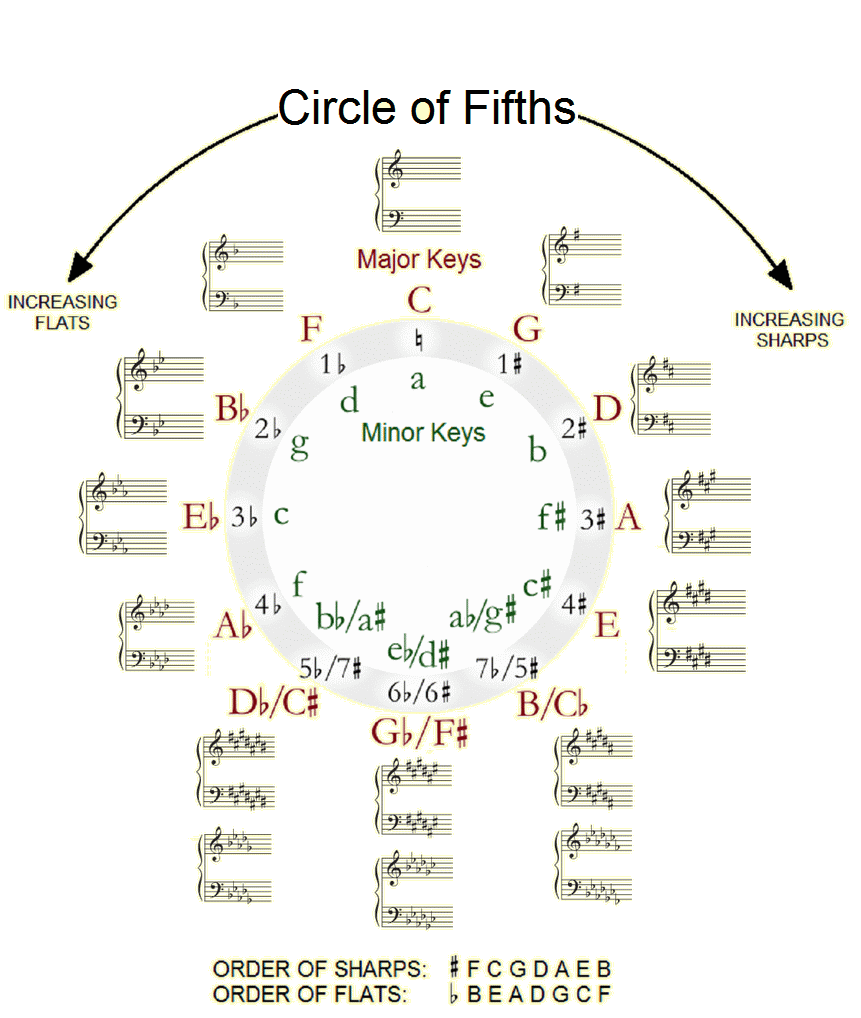
The Circle of Fifths is a geometric representation of how the 12 notes of the chromatic scale relate to one another. If you look closely at the diagram you will see each note is a Perfect Fifth (seven semitones, or seven frets on the fretboard) higher than the next (going clockwise).
Not sure what is a Perfect Fifth? Then, before going forward, you should take a look at our tutorial on music intervals . It will explain what intervals are and how to find them on the fretboard.
The G is a fifth away from the C in the major scale. Going clockwise on the Circle of Fifths the next note will always be a fifth away. Now if we move counterclockwise on the Circle of Fifths, we are a fourth away, F is the fourth note of the C major scale.
So our clockwise sequence is:
- C
- G
- D
- A
- E
- B
- F#
- C#
- Ab
- Eb
- Bb
- F
- C
As always music theory can quickly get a little garbled which is why the Circle of Fifths is so very helpful. It allows you to quickly see how each note in the scale relates to the next , and how it all falls into a convenient loop or circle.
How To Memorize the Circle Of Fifths: Memory Trick for Guitar Players
Now here's a little trick for memorizing the Circle of Fifths with the help of the guitar fretboard.
If you know your guitar notes names , it will be easy to follow the Cof (Circle of Fifths) right on the neck. We start from the C at the 3rd fret of the A string , and we go up by one Perfect Fifth, note after note. With the help of fretboard octaves (again, if you don't know what octaves are, please go to the music intervals tutorial) our Circle Of Fifths can be laid out horizontally in the pattern shown here below:
No need to memorize the Circle of Fifths if you know your fretboard notes!
Awesome! We see that it's enough to learn this fretboard pattern for knowing the sequence of the notes in the Cof!
Just don’t forget that when we move:
- clockwise (left to right on the fretboard pattern), we are moving in fifths,
- counterclockwise , we are moving in fourths (right to left on the fretboard pattern)
Before approaching sharps and flats, We need to clarify what enharmonics are. If you are already familiar with the subject, feel free to skip this section.
In western music, there are 12 notes in the chromatic scale, each one a semitone away from each other. On your guitar, each fret represents one of these notes and every fret is one semitone. These notes in the chromatic scale are;
- C
- C#/Db
- D
- D#/Eb
- E
- F
- F#/Gb
- G
- G#/Ab
- A
- A#/Bb
- B
- and then back to C
The notes with a slash are known as enharmonic notes , and they are the same pitch as each other. For example, C# is enharmonically equivalent to Db they are just spelled differently. Depending on which key you are in will determine the spelling.
If you are in the key of E then you will spell the note C#, if in the key of Ab than you will spell the note as Db.
Now, of course, this can cause some immediate confusion, which is why we have the Circle of Fifths.
How to use the Circle of Fifths to organize music keys
The Circle of Fifths packs an awful lot of data into a small circle. On the outside are the names of the major keys while on the inside are the names of the minor keys.
As we mentioned above the key of G is five steps above the key of C, and just as well the key of Em is five steps above the key of Am. (If you use your fingers to count each note alphabetically you will see they each interval adds up to five).
The CoF also will denote how many sharps or flats are in each key. The sharps are on the right side and the flats on the left. Starting at the top with C we have no sharps or flats as there are none in the C major scale.
From there each fifth adds another sharp, until we reach the bottom and then it goes backwards with flats until we come back to C again.
Now you will notice at the bottom of the CoF that some keys have different spellings and can either be denoted with sharps or flats.
Remember from above that these are enharmonically equivalent it just depends on which the composer wishes to use. If you are not sure how many sharps the Key of B has, well just count from the beginning of the CoF (excluding the natural key of C) and you will have five sharps.
If you want to know how many flats are in the enharmonic equivalent of B, which is Cb, well count backwards and you will get 7 flats.
By knowing the number (if any) of sharps or flats, we will have the key signature readily available by the CoF. (As you read on keep checking back with the Circle of Fifths tool , that way you understand exactly what is written. The Cof is so wonderful because it simplifies all of this!)
Sharp keys: follow the CoF clockwise, one 5th at a time

| Key | Sharps | Notes |
|---|---|---|
| C | 0 | - |
| G | 1 | F# |
| D | 2 | F# C# |
| A | 3 | F# C# G# |
| E | 4 | F# C# G# D# |
| B | 5 | F# C# G# D# A# |
| F# | 6 | F# C# G# D# A# E# |
| C# | 7 | F# C# G# D# A# E# B# |
The sharps are added a 5th away each other. Notice that the new sharp is the root of the tonic one semiton below (G key, F#

| Key | Flats | Notes |
|---|---|---|
| F | 1 | Bb |
| Bb | 2 | Bb Eb |
| Eb | 3 | Bb Eb Ab |
| Ab | 4 | Bb Eb Ab Db |
| Db | 5 | Bb Eb Ab Db Gb |
| Gb | 6 | Bb Eb Ab Db Gb Cb |
| Cb | 7 | Bb Eb Ab Db Gb Cb Fb |
The flats apper a 4th away from each other
How to create chord progressions with the help of the Circle of Fifths
Now let’s work on building some chord progressions.
First a quick trick on how to find any major scale using the Cof.
To find the C scale we simply go counterclockwise one step and then count seven clockwise .
So one step counterclockwise is F and then counting forward C, G, D, A, E, and B. And there you have the C major scale. This works the same for every major scale, move back one and then up seven. (Of course after you find the right scale it helps to put it in order).
Chords Degrees
There are a few different methods to build chord progressions using the CoF. First though we need to remind ourselves of the Nashville Number System and Romand Numerals Notation .
It was devised as a way to show scale degrees to those musicians who knew little about music theory. However, it turns out that it is also a handy system to teach said theory!
To find the chords of a key, just rotate the degrees
Major Scale Degrees
| Scale | I | ii | iii | IV | V | vi | vii° |
|---|---|---|---|---|---|---|---|
| Major | Major | Minor | Minor | Major | Major | Minor | Half-Diminished |
| Scale | i | ii° | III | iv | v | VI | VII° |
|---|---|---|---|---|---|---|---|
| Minor | Minor | Half-Diminished | Major | Minor | Minor | Major | Major |
Chord Progressions
Now the numbers are written in Roman numerals so you will see a major key notated like;
- I
- ii
- iii
- IV
- V
- vi
- vii°
One of the most popular progressions ever in music is the I-IV-V or the 1-4-5 , depending on how it is shown. Since we have been dealing so exclusively with the key of C, lets change it up to test our CoF knowledge. We will find the 1-4-5 progression for the key of D .
Remember when we move backwards on the circle we move in fourths, forwards we move in fifths. So if we look at D it’s easy to see the fourth behind it is G and the fifth in front is an A. The 1-4-5 chords for the key of D is D-G-A .
If you happen upon a band jamming in 1-4-5 or I-IV-V all you need to know is the key and your CoF and you are golden.
Now here is another way to find your 1-4-5. First find the D major scale, to find that we move one back and count forward seven;
G D A E B F# C# if we put it in order D E F# G A B C# and the 1-4-5 of this scale is again D-G-A.
I-V-vi-IV Chord Progression
This method helps if we want to find more complicated progressions. Another super common pop music progression is I-V-vi-IV or 1-5-6-4, so in the key of D that is D-A-Bm-G .
Now try to find the Doo Wop progression I-vi-IV-V or 1-6-4-5 for the key of Eb. One back and seven forward gets us;
Ab Eb Bb F C G D put in order we get Eb F G Ab Bb C D so the Doo Wop progression in the key of Eb is Eb-Cm-Ab-Bb .
How to use the Circle of Fifths to change key
Creating songs with chords that belong to the same keys can work, but if we want to be creative, during the song, we can modulate to other keys . That means our song will have chords that belong to more than one key. Let's see how to use the Circle of Fifths for key modulation.
Modulate to the relative minor key
And a very quick way to tell the minor corresponding key to each major key is simply the inner circle. The C major key has a relative minor of A , and so on for each note on the CoF. Now this is known as modulating to a relative key. And that is our next lesson on the CoF.
In music modulating is moving from one key to another, or also put as moving from one tonic (root) to another tonic.
So modulating to the relative key is very simple as its clearly written out right as you look at the CoF. The modulated relative keys will have the same key signatures.
This change can be difficult to notice for the listener.
Now what of we wanted to modulate to a parallel key ? This is another very easy thing to do as the parallel key of a C major is simply a C minor . They can trade places in a song when necessary as they both share the dominate chord.
Modulate to a close key
We can also modulate to another closely related key . To do this we find keys that have similar notes to one another. This is very simple with the CoF as all we need to do is look at the keys that are beside them . The key of G and the key of D have many similar notes and thus can make a great and workable change in a song.
A good way to make this change to a closely related key would be using a similar chord that both keys share . When switching from the key of G to D we can use the D major chord as both keys share this chord making a smooth transition.
You can also modulate by step if you like, but you first have to find the scale of the key you are in. Once you find it you can modulate by half steps or whole steps if you like. So moving from C major to C# major would be a half step modulation. Which follows C major to D major would be a whole step modulation.
There is even a form of chain modulation by using various ideas from above mixed. For example you can start with closely related keys , change to parallel keys , and then add on a relative key change to get these specific key changes in your song:
C G D C Cmin Eb
Did you already download your free pdfs?
Download Your Free Learning Resources
How to transpose songs
Along with scales, key signatures, chord building, and modulation, we can also use the CoF to transpose our songs . Now some transposing involves changing the notes so it will fit the pitch of the instrument.
Normal concert pitch is in C, and some woodwinds and brass instruments are in the pitches of Bb, Eb, and F. However as guitar players we will basically always be in concert pitch so this form of transposition will not be used often.
Instead we may have to change the key signature of the chords or the progressions. As we have shown above this can be done in a variety of ways through finding the scales, or modulating. With the CoF we can accomplish just about any musical task.
Transposing a song 1 whole-step up (from C to D)
The easiest way to transpose a song from one key to another, is to set the root of the new key as degree I in the Circle of Fifths, and find the chords as seen below.
| Scale | I | ii | iii | IV | V | vi | vii° |
|---|---|---|---|---|---|---|---|
| Major | Major | Minor | Minor | Major | Major | Minor | Half-Diminished |
How to construct chord with the Circle Of Fifths
So far we can tell the way in which each note relates and the different key signatures by the CoF, but we can also build entire chords and chord progressions with it.
To review, a major chord or triad is made up of the root, third, and fifth. Now to find a C major chord we take the C scale;
C D E F G A B C
- The root is C
- The third is E
- The fifth is G
If we connect these on the CoF we get a triangle shape. If you move this exact same shape in any direction you will get other major chords.
Construct Minor Chords
If you want to find a minor chord like C minor (root, minor 3rd, and fifth);
C Eb G The triangle image is reversed
We also have triangle shapes for diminished and augmented chords . Remember a dim chord is root, minor third, and a flattened fifth. And an augmented chord is the root, major third, and sharp fifth.
As an exercise, try to find those shapes on the circle!
Circle Of Fifths Diagram
If you memorize these shapes you will be able to move the triangles in any direction to find the notes of other chords. There also some quadrilateral shapes that can be moved to find various chords.
We can extend this concept and construct four chords notes:
- A major seventh chord is made up of the root, major third, perfect fifth, and major seventh.
- A minor seventh is the root, minor third, perfect fifth, and minor seventh.
- The seventh chord is simply made up of the root, major third, perfect fifth, and minor seventh.
Ninth chords do have moveable five sided shapes, but that can get a little complicated when shifting it. After time and practice with triangle and trapezoid shapes eventually you will be able to visualize the building blocks of most every chord on the CoF.
CIRCLE OF FIFTHS AND MODES
Earlier we mentioned finding major scales with the CoF, we kept it easy with only that scale. However now that you have a better grasp on the CoF let’s take a final look at how to find all other scales or modes . There are seven modes in western music;
- Ionian: starts on the first note of major scale
- Dorian: starts on second note of major scale
- Phrygian: starts on third note
- Lydian: fourth note
- Mixolydian: fifth note
- Aeolian: sixth note
- Locrian: seventh note
These scales or modes are what give music that certain feel or mood to a song. An Ionian major scale like we already learned above will have an upbeat and happy sound , while the Aeolian will have a minor and melancholy type feel. Play each mode to get an idea of how they sound.
And how do we use the CoF to find these modes?
With C at the top of the circle this chart shows us which note will be which mode. G comes after C on the CoF, and G is a fifth above C, thus G will be the start of the mixolydian scale !
And of course like all aspects of the CoF we simply rotate these words for each scale . Just like with the shapes, scales, and some modulations from above rotating is the key to the CoF! If you want to learn more about modes, don't miss our interactive tutorial on modes for guitar
Interactive Tool To Learn The Circle of Fifths
As the Circle of Fifths becomes easier to grasp you will truly see that it is not only useful as a music tool, it is absolutely essential. If you want your guitar playing and music knowledge to soar to great heights, you will get to know every aspect of the CoF!
Music Circle Of Fifths Diagram
To help you study further here is an interactive tool to help you practice the Circle of Fifths. Enjoy!
Circle Of Fifths Diagram Guitar
To stay updated on new tutorials, subscribe to the free newsletter (you'll also get access to the download area with lots of free printable resources)